Описание
Математика ответы Синергия СПО Колледж темы 1-14 экзамен на “Отлично” 92/100 баллов
УЧЕБНЫЕ МАТЕРИАЛЫ
Введение в курс
Тема 1. Комплексные числа и действия над ними
Тема 2. Матрицы, определители
Тема 3. Системы линейных управлений.
Тема 4. Прямая на плоскости и ее уравнение
Тема 5. Кривые второго порядка
Тема 6. Теория пределов
Тема 7. Производная и дифференциал
Тема 8. Неопределённый интеграл
Тема 9. Определённый интеграл
Тема 10. Дифференциальные уравнения
Тема 11. Множества. Отношения
Тема 12. Элементы теории вероятностей
Тема 13. Элементы математической статистики
Тема 14. Приближенные числа и действия с ними
Заключение
Итоговая аттестация
Значение выражения і⁴ равно …
Квадрат модуля комплексного числа 2 + 3і равен …
Комплексно-сопряженным для числа 2 – 8і является число …
Мнимая часть комплексного числа (InZ) z = 2 + 3і равна …
Произведение чисел (1 – 2i)(3 + 4i) равно …
11 – 2i
3 – 8i
11 + 2i
Соотнесите формы комплексного числа с их видом:
Алгебраическая форма
Показательная форма
Тригонометрическая форма
z=a+ib
z = | z | e^iφ
z=|z|·(cos(φ)+isin(φ))
Сумма комплексных чисел 2 – 9і и 6 – і равна …
8 + 10i
–7 + 5i
8 – 10i
Упорядочьте комплексные числа по возрастанию мнимой части:
1 1 – 3i
2 –2 + 4i
3 5i
Ученику необходимо вычислить z⁻³, если z = 1 – i.
Какой ответ окажется верным?
–0,25 + 0,25i.
–0,25 – 0,25i.
0,25 – 0,25i.
Число 3-4i представимо в тригонометрической форме в виде …
5(cosф + isinф)
7(cosф + isinф)
3cosф – 4isinф
Число 6+2i представимо в показательной форме в виде …
6cosф + 2isinф
√40e^iф
40eiф
Даны матрицы ((8, –4), (–5, 0)) и ((1, –7), (4, 9)).
Найдите значение выражения A² – Bᵀ.
((75, 36), (–16, 11)).
((83, –36), (–33, 11)).
((–83, 36), (33, –11)).
Матрица ((1, 1, 1), (1, 0, 1), (1, 1, 1), (1, 1, 1)) имеет размерность …
4х4
3х3
4х3
Матрица А называется … с матрицей В, если число столбцов матрицы А равно числу строк матрицы В
Матрица порядка n имеет … миноров (n-1)-го порядка
n+1
n²
n
Понятие определителя вводится для … матриц
треугольных
квадратных
ступенчатых
Пусть дана матрица А = ((2, 3), (4, –5)), тогда ее определитель равен …
22
-25
-22
Разностью матриц A и B называется … матрицы A с матрицей, противоположной матрице B
Сопоставьте размерность матрицы и формулу для вычисления ее определителя:
A(1×1)
A(2×2)
A(3×3)
a₁₁
a₁₁a₂₂ – a₁₂a₂₁
Σ (−1)ᵏ⁺¹a₁ₖM₁ₖ
Число, которое вычисляется по формуле a₁₁ · a₂₂ – a₁₂ · a₂₁ для матрицы A = ((a₁₁, a₁₂), (a₂₁, a₂₂)) называется …
Числовой матрицей размера m х n называется …
четная или нечетная числовая функция
прямоугольная таблица m х n чисел, состоящая из m строк и n столбцов
вектор
Матрица называется … матрицей, если в каждой ее ненулевой строке имеется такой ненулевой элемент, что все остальные элементы столбца, содержащего этот элемент, равны нулю
Пусть дана система уравнений {x − y = −1, 2x + y = 7, тогда сумма решений (x + y) этой системы равна …
Пусть дана система уравнений {3x + 2y − 4z = 8, 2x + 4y − 5z = 11, 4x − 3y + 2z = 1.
Найдите сумму корней x+y+z.
9
7
6
Пусть дана система уравнений A = {2x₁ + 2x₂ + x₃ = −6, 3x₁ + 2x₂ − x₃ = −8, 4x₁ − x₂ − x₃ = −7, тогда определитель |A| этой системы равен …
-19
-20
-22
Пусть дана система уравнений A = {2x₁ + 2x₂ + x₃ = −6, 3x₁ + 2x₂ − x₃ = −8, 4x₁ − x₂ − x₃ = −7, тогда определитель |A₁| этой системы равен …
44
40
38
Пусть дана система уравнений A = {2x₁ + 2x₂ + x₃ = −6, 3x₁ + 2x₂ − x₃ = −8, 4x₁ − x₂ − x₃ = −7, тогда определитель |A₂| этой системы равен …
Пусть дана система уравнений A = {2x₁ + 2x₂ + x₃ = −6, 3x₁ + 2x₂ − x₃ = −8, 4x₁ − x₂ − x₃ = −7, тогда определитель |A₃| этой системы равен …
1
0
-1
Пусть дана система уравнений A = {2x₁ + 2x₂ + x₃ = −6, 3x₁ + 2x₂ − x₃ = −8, 4x₁ − x₂ − x₃ = −7, тогда решение этой системы (x₁, x₂, x₃) равно …
Расположите выражения, известные для системы линейных уравнений (см. ниже), в следующем порядке: «основная матрица системы, матрица неизвестных, матрица правой части»: {2x₁ + 3x₂ + 4x₃ + x₄ = 1, x₁ + 4x₂ + 3x₃ + 2x₄ = 3, 7x₁ + 5x₂ + 6x₃ + 7x₄ = 2
1 ((2, 3, 4, 1), (1, 4, 3, 2), (7, 5, 6, 7))
2 ((x₁), (x₂), (x₃))
3 ((1), (3), (2))
Система уравнений {x₁ − 2x₂ + 3x₃ = 0, −x₁ + 2x₂ + 4x₃ + 3x₄ = 0, −5x₂ + 2x₄ = 0 имеет …
одно решение
бесконечно много решений
ни одного решения
Установите соответствие понятия и его характеристики:
Совместная система уравнений
Несовместная система уравнений
Определенная система уравнений
система уравнений, имеющая хотя бы одно решение
система уравнений, не имеющая решений
совместная система уравнений, имеющая единственное решение
Два ненулевых вектора на плоскости называются … , ели они лежат либо на одной прямой, либо на параллельных прямых
Две прямые y₁ = 3x + 5 и y₂ = −2x + 1 на плоскости …
пересекаются
параллельны
совпадают
Каноническое уравнение прямой, проходящей через точки A(1,3) и B(−2,5), имеет вид …
(x−2)/(−2) = (y−3)/2
(x−1)/(−3) = (y−3)/2
(x+3)/(−2) = (y−2)/(−3)
На плане местности изображена дорога и дерево, стоящее в стороне. Чтобы вычислить кратчайшее расстояние от дерева до дороги на карте ввели систему координат: дерево представили точкой с координатами A(1,5), дорогу представили прямой с уравнением 3x – 4y – 3 = 0.
Найдите расстояние от дерева до дороги.
Расстояние равно 6.
Расстояние равно 5.
Расстояние равно 4.
Расположите прямые y₁, y₂ и y₃, заданные уравнениями, в порядке убывания их угловых коэффициентов:
1 y₂ = x + 2
2 y₁ = –x – 3
3 y₃ = –3x
Скалярным произведением двух векторов называется произведение их длин на … угла между ними
Сопоставьте способ задания прямой на плоскости и ее уравнение:
Общее уравнение прямой
Известны точка M(x₀, y₀) и нормаль n(A, B)
Известны точка M(x₀, y₀) и направляющий вектор l(A, B)
Ax + By + C = 0
A(x − x₀) + B(y − y₀) = 0
(x − x₀) / A = (y − y₀) / B
Сумма координат точки пересечения прямых y₁ = 3x + 2 и y₂= x + 1 равна …
Уравнение прямой, проходящей через точки A(1,3) и B(1,5), имеет вид …
x = 1
x = −1
y = 1
Уравнение прямой, проходящей через точки A(2,3) и B(0,5), имеет вид …
y = 2x − 3
y = −5x + 1
y = –x + 5
Уравнение прямой с угловым коэффициентом, проходящей через точки A(1,3) и B(−2,5), имеет вид …
y = (–2/3)x + 11/3
y = (2/3)x + 11/3
y = (–2/3)x – 11/3
Величина p в уравнении кривой (y – y₀)² = ± 2p · (x – x₀) называется …
фокус
параметр
директриса
Дано: расстояние между вершинами равно 8, расстояние между фокусами равно 10.
Составьте уравнение гиперболы, оси которой совпадают с осями координат.
x²/16 – y²/9 = 1.
x²/25 – y²/16 = 1.
x²/64 – y²/25 = 1.
Действительная ось (Оу) и мнимая ось (Ох) гиперболы равны 8 и 6 соответственно, тогда координаты фокусов гиперболы равны …
F₁,₂ (±5; 0)
F₁,₂ (0; ±10)
F₁,₂ (0; ±5)
Кривая, состоящая из всех точек плоскости, сумма расстояний от которых до двух данных точек (фокусов) есть величина постоянная, называется …
Кривая второго порядка, имеющая асимптоты, – это …
Кривая второго порядка, имеющая радиус – это …
окружность
эллипс
гипербола
Расположите условия взаимного расположения точки M(x₁,y₁) и окружности x² + y² = R² в следующем порядке: «точка лежит на окружности, точка лежит вне окружности, точка лежит внутри окружности»:
1 x₁² + y₁² = R²
2 x₁² + y₁² > R²
3 x₁² + y₁² < R²
Расстояние от точки, лежащей на параболе, до фокуса равно 6, тогда расстояние от этой точки до директрисы равно …
Сопоставьте уравнения кривой второго порядка и его описание:
y² = ±2p · x
x²/a² + y²/b² = 1
x² + y² = R²
уравнение параболы с вершиной в начале координат
уравнение эллипса с центром в начале координат
уравнение окружности с центром в начале координат
Уравнение x²/16 + y²/16 = 1 задает …
гипербола
окружность
эллипс
Фокусы эллипса находятся …
на малой оси внутри эллипса
снаружи эллипса на большой оси
внутри эллипса на большой оси
Бесконечно большой функцией при х ⟶ 0 является …
y(x) = (x – 3)²
y(x) = 1/x²
y(x) = x³
Бесконечно малой функцией при х ⟶ 3 является …
y(x) = 1/x²
y(x) = x³
y(x) = (x – 3)²
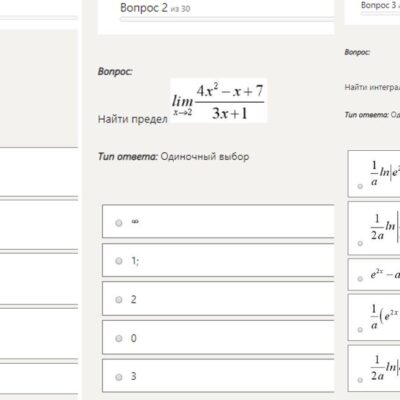
Данный предел lim (7x² + 4x − 3) / (2x² + 3x + 1), x⟶−2 равен …
15/3
17/3
14/3
Значение предела lim (2x⁵ − 3x³ + 1) / (x⁵ + 4x² + 2x), x⟶∞ равно …
Предел функции lim (–eˣ⁻² + x² + 3x) , x⟶2 равен …
Предел функции lim (1 + 3x + x²) / (x + 4), x⟶∞ равен …
5
∞
0
Предел функции lim (3x + 1) / (2x – 1), x⟶1 равен …
Предел функции lim (6 + 3x + x²) / (2 + x – x²), x⟶∞ равен …
-1
0
1
При нахождении предела lim (√(x – 2) – √x), x⟶∞ студент понял, что имеет дело с неопределенностью вида [∞/∞].
Он решил раскрыть эту неопределенность умножив и разделив на сопряженное выражение.
Решите данный предел и укажите ответ.
0
∞
-1
Расположите обозначения в следующем порядке: «область определения функции, область значений функции, значение функции в точке»:
1 D(f)
2 E(f)
3 f(x₀)
Сопоставьте свойства пределов и их значения:
lim c ⋅ f(x), x⟶x₀
lim (f(x) + g(x)), x⟶x₀
lim f(x) / g(x), x⟶x₀
c ⋅ lim f(x), x⟶x₀
lim f(x), x⟶x₀ + lim g(x), x⟶x₀
lim f(x), x⟶x₀ : lim g(x), x⟶x₀
… функции y = f(x) в точке x называется главная, линейная относительно Δx часть приращения функции в этой точке: dy = y(x)’Δx
График функции y = f(x) называется … на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале
Мгновенная скорость материальной точки, движущейся прямолинейно по закону s = 3sin(2t – 2) в момент t=1 равна …
Необходимое условие достижения функцией f(x) экстремума в точке x …
f(x) = 0
f ‘(x) = 0
f ‘(x) = 1
Производная второго порядка от функции y = x^7 равна …
y” = 7×6
y” = 42x⁵
y” = x⁵
Производная сложной функции y = cos³x равна …
Производная сложной функции y = e^(sin x) равна …
sinxe^(sin x−1)
cosxe^(sin x)
e^(cos x)
Производная функции у = 3х³ + 2x² − 5x + 7 равна …
9x² + 4x – 5
21x² − 4x + 5
−21x² − 4x − 5
Пусть дана функция y = (3x² − 1)⁵.
Укажите верное рассуждения при нахождении ее производной.
Пусть 3x² − 1 = u, тогда y = u⁵. По теореме о производной сложной функции y’ = (u⁵)’ = 5u⁴; u’ = (3x² − 1)’ = 6x. Тогда y’ = 5(3x² − 1)⁴6x = 30x(3x² − 1)⁴.
Пусть 3x² − 1 = u, тогда y = u⁵. По теореме о производной сложной функции y’ = (u⁵)’ = 5u⁴; Тогда y’ = 5(3x² − 1)⁴.
Пусть 3x² − 1 = u, тогда y = u⁵. По теореме о производной сложной функции y’ = (u⁵)’ = 10u Тогда y’ = 10.
Расположите значения производных для функций в следующем порядке: «y = xⁿ, y = aˣ, y = √x»:
1 y’ = n ⋅ xⁿ⁻¹
2 y’ = aˣ ⋅ lna
3 y’ = 1 / 2√x
Сопоставьте правила дифференцирования и их формулы:
(u + v)’
(u ∙ v)’
(u / v)’
u’ + v’
u’v + uv’
(u’v − uv’) / v²
Дан неопределенный интеграл ∫ (5х³ − 4cosx + 3/sin²x)dx.
Укажите правильное решение.
∫ (5х³ − 4cosx + 3/sin²x)dx = ∫5х³dx − ∫4cosxdx + ∫3/sin²xdx = 5∫xdx − 4∫cosxdx + 3∫dx/sin²x = 5 · x/4 – 4cosx – 3ctgx + C.
∫ (5х³ − 4cosx + 3/sin²x)dx = ∫5х³dx − ∫4cosxdx + ∫3/sin²xdx = 5∫x³dx − 4∫cosxdx + 3∫dx/sin²x = 5 · x⁴/4 – 4sinx – 3ctgx + C.
∫ (5х³ − 4cosx + 3/sin²x)dx = ∫5х³dx − ∫4cosxdx + ∫3/sin²xdx = 5∫x³dx − 4∫cosxdx + 3∫dx/sin²x = 5 · x⁴/4 – 4cosx – 3ctgx + C.
Множество всех первообразных функции f(x) называется … от этой функции (укажите словосочетание)
Неопределенный интеграл ∫ (3x+8)^6dx равен …
1/3 (3x+8)^7 + C
1/7 (3x+8)^7 + C
1/21 (3x+8)^7 + C
Неопределенный интеграл ∫ x^10dx равен …
x^11 + C
x^11 / 11 + C
1/10 x^11 + C
Неопределенный интеграл ∫ x(1 − 2x)³dx равен …
2x⁴ + C
-8x⁵/5 + C
−2x³ + 3x⁴ − 8x⁵/5 + C
Неопределенный интеграл ∫ xeˣdx равен …
xeˣ − eˣ + C
xeˣ + eˣ + C
x²eˣ − eˣ + C
Постоянный множитель, можно … за знак интеграла
Равенство ∫udv = uv − ∫vdu называют формулой интегрирования по …
Расположите первообразные для данных функций в следующем порядке: «3x², 4x³, 5x⁴»:
1 x³ + C
2 x⁴ + C
3 x⁵ + C
Сопоставьте интеграл от элементарной функции и его значение:
∫ dx/x
∫ sinxdx
∫ dx/cos²x
ln|x| + C
−cosx + C
tgx + C
Функция F(x) называется … для функции f(x), если F(x)’ = f(x)
В формуле Ньютона-Лейбница ∫ f(x)dx, x=a..b равен …
F(a) − F(b)
F(b) – F(a)
F(a) + F(b)
Дан определенный интеграл ∫ √(2x – 10)dx, x=7..23.
Укажите правильный выбор метода его решения.
Необходимо сделать замену: пусть √(2x – 10) = t → 2x – 10 = t².
Данный интеграл решается методом по частям: u = √x, v = 2x – 10.
Данный интеграл решается подстановкой пределов интегрирования без каких-либо преобразований подынтегральной функции.
Интеграл ∫ √2/x dx, x=1..e равен …
−√2
0
√2
Интеграл ∫ (x + 1)(x – 1)dx, x=1..1 равен …
Интеграл ∫ x⁴dx, x=0..1 равен …
Непрерывность функции является … условием ее интегрируемости
Определенный интеграл ∫ x⁻⁴dx, x=1..+∞ равен …
1/3
3
1
Определенный интеграл ∫ x / √(1 + x)dx, x=3..8 равен …
1/2
7/5
32/3
Расположите значения интегралов в порядке возрастания:
1 ∫ x²dx, x=1..2
2 ∫ x⁴dx, x=1..2
3 ∫ (3 − 2x − x²)dx, x=-2..1
Сопоставьте свойства определенного интеграла и их записи:
Обе части неравенства можно почленно интегрировать
При перестановке пределов интеграла интеграл меняет свой знак
Значение определенного интеграла равно, при некотором c ϵ (а, b), площади прямоугольника с высотой f(c) и основанием b-a
a<b, f(x) ≤ g(x), то и ∫f(x)dx ≤ ∫g(x)dx
∫ f(x)dx, x=a..b = ∫ f(x)dx, x=a..–b
∫ f(x)dx, x=a..b = f(c)·(b – a)
Число a в записи ∫ f(x)dx, x=a..b называется … пределом интегрирования
Дано дифференциальное уравнение y” + 6у’ + 9у = 0.
Укажите верное решение.
Характеристическое уравнение данного дифференциального уравнения имеет вид k² + 6k + 9 = 0.
Корни характеристического уравнения k₁ = k₂ = –3.
Получаем общее решение вида C₁e⁻³ˣ + C₂xe⁻³ˣ.
Характеристическое уравнение данного дифференциального уравнения имеет вид –k² – 6k – 9 = 0.
Корни характеристического уравнения k₁ = k₂ = 3.
Получаем общее решение вида C₁e³ˣ + C₂xe³ˣ.
Характеристическое уравнение данного дифференциального уравнения имеет вид k² + 6k + 9 = 0.
Корни характеристического уравнения k₁ = 3, k₂ = –3.
Получаем общее решение вида C₁e³ˣ + C₂e⁻³ˣ.
Дискриминант характеристического уравнения данного дифференциального уравнения y” + 5y’ – 6y = 0 равен …
Дискриминант характеристического уравнения дифференциального уравнения y” – 5y’ + 6y = 0 равен …
-1
0
1
Задачей … называется задача нахождения такого решения уравнения, при котором интегральная кривая решения проходит через точку с координатами (x₀, y₀)
Наивысший порядок производной неизвестной функции, входящей в уравнение, называется … уравнения
Общее решение дифференциального уравнения (1 + x²)dy + ydx = 0 имеет вид …
y = e^(–arctgx)
y = Ce^(–arctgx)
y = –lnx + C
Общее решение дифференциального уравнения y’ = y равно …
y = x + C
y = Ceˣ
y = sinx + C
Общее решение уравнения y’ + 4y = 0 имеет вид …
y = c₁e²ˣ + c₂e²ˣ
y = c₁ + e²ˣ
y = c₁cos2x + c₂sin2x
Расположите данные дифференциальные уравнения в следующем порядке: «дифференциальное уравнение 1-го порядка, дифференциальное уравнение 2-го порядка, дифференциальное уравнение 3-го порядка»:
1 y’ – 3y = 2x
2 y” – xy = 0
3 y”’ + 3y’ + 0
Сопоставьте дифференциальное уравнение первого порядка и его общим вид:
С разделенными переменными
С разделяющимися переменными
Однородное
f(y)dy = f(x)dx
f₁(x)g(y)dx = f₂(x)dy
P(x,y)dx = Q(x,y)dy
Условием существования двух действительных корней характеристического уравнения дифференциального уравнения является дискриминант характеристического уравнения, который …
больше нуля
равен нулю
меньше нуля
Верным будет утверждение, что …
√3 ϵ N
3 ϵ N
-3 ϵ N
Даны множества A = {a, b, c}, B = {1, 2}, C = {2, 3, 4}.
Запишите множества А × В; А × С и В × С.
A × B = {(a, 1), (a, 2), (b, 2), (c, 1), (c, 2)}.
A × C = {(a, 2), (a, 3), (a, 4), (b, 2), (c, 2), (c, 3), (c, 4)}.
B × C = {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}.
A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}.
A × C = {(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4), (c, 2), (c, 3), (c, 4)}.
B × C = {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}.
A × B = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2), (a, a)}.
A × C = {(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4), (c, 2), (c, 3), (c, 4), (a, c)}.
B × C = {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)}.
Декартовым произведением множеств {1, 2} и {А, Б} является множество …
{(1, А), (1, Б), (2, А), (2, Б)}
{(1, А), (2, 1), (1, Б), (2, Б)}
{(А, 1), (А, 2), (Б, А), (А, Б)}
Множество, равномощное множеству натуральных чисел, называется … множеством
Множество, содержащее только общие элементы двух множеств, называется … данных множеств
Множество {10, 20, 30, 40, 50} содержит … элементов
На множестве целых чисел задано отношение неравенством: 3x – 2y ≤ 0.
Данному отношению принадлежит следующая пара чисел …
(1; –2)
(2; 0)
(1; 2)
Пустое множество содержит … элементов
Совокупность всех подмножеств множества А называется …
булеан А
мощность А
область определения А
Соотнесите свойства множеств с их математическими выражениями:
Коммутативность
Идемпотентность
Ассоциативность
A ∪ B = B ∪ A
A ∪ A = A
(A ∪ B) ∪ C = A ∪ (B ∪ C)
… вероятность – это вероятность наступления события A, вычисленная в предположении, что событие B уже произошло
… события A называется отношение числа исходов m, благоприятствующих наступлению события A к числу всех возможных исходов n
Вероятность наступления некоторого события не может быть равна …
0
1
-1
Два стрелка производят по одному выстрелу. Вероятности попадания в цель для первого и второго стрелков равны 0,5 и 0,4 соответственно. Тогда вероятность того, что в цель попадут оба стрелка, равна …
0,2
0,3
0,4
Игральная кость бросается один раз, тогда вероятность того, что на верхней грани выпадет не менее трех очков, равна …
2/3
1/3
1/6
Из урны, в которой находятся 4 белых и 7 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет белым, равна …
7/11
4/11
11/11
Несколько событий называют … , если возможно появление только одного из событий
По оценкам экспертов вероятности банкротства для двух предприятий, производящих разнотипную продукцию, равны 0,1 и 0,35, соответственно. Тогда вероятность банкротства обоих предприятий равна …
0, 035
0,055
0,35
Расположите формулы в следующем порядке: «формула Бернулли, формула Байеса, формула классической вероятности»:
1 Pn(k) = n! / k!(n–k)! · pk · qn–k
2 p(Bi/A) = p(Bi)·p(A/Bi) / p(A)
3 P(A) = m/n
Сопоставьте событие и его характеристику:
После зимы наступит весна
После весны наступит весна
Завтра пойдет дождь
достоверное событие
невозможное событие
случайное событие
Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке четное.
Укажите верное решение.
Используем классическое определение вероятности: P=m/n, где n – число всех возможных элементарных исходов, m – число элементарных исходов, благоприятствующих осуществлению события. В нашем случае, n = 9, так как всего 9 различных карточек. m = 5, так как всего на 4 карточках написаны четные числа (2, 4, 5, 6, 8). Тогда Р=5/9.
Используем классическое определение вероятности: P=n/m, где n – число всех возможных элементарных исходов, m – число элементарных исходов, благоприятствующих осуществлению события. В нашем случае, n = 9, так как всего 9 различных карточек. m = 4, так как всего на 4 карточках написаны четные числа (2, 4, 6, 8). Тогда Р=9/4.
Используем классическое определение вероятности: P=m/n, где n – число всех возможных элементарных исходов, m – число элементарных исходов, благоприятствующих осуществлению события. В нашем случае, n = 9, так как всего 9 различных карточек. m = 4, так как всего на 4 карточках написаны четные числа (2, 4, 6, 8). Тогда Р=4/9.
В одном испытании случайная величина принимает одно и только одно возможное значение, значит, сумма вероятностей этих событий равна …
Дан закон распределения вероятностей дискретной случайной величины Х (см ниже). Тогда значение a равно …
0,3
0,7
-0,3
Дискретная случайная величина X задана законом распределения вероятностей (см. таблицу ниже). Тогда математическое ожидание случайной величины Y = 3X равно …
5,1
6
5,7
Задан закон распределения дискретной случайной величины X (см. ниже).
Найдите математическое ожидание, дисперсию и среднее квадратичное отклонение.
42,4; 2,04; 1,43.
40,4; 2,15; 1,56.
41,65; 2,98; 1,32.
Закон распределения вероятностей дискретной случайной величины X показан в таблице (см. ниже), тогда a равно …
0,9
0,8
0,2
Законом распределения дискретной случайной величины называется между значениями x₁,x₂,…,xn (пусть число значений конечно) этой случайной величины и их вероятностями p₁,p₂,…,pn
Известно, что M(X) = 2, тогда математическое ожидание случайной величины Y = 5X – 3 равно …
Пусть X – дискретная случайная величина, заданная законом распределения вероятностей (см. ниже). Тогда математическое ожидание этой случайной величины равно…
1,8
2,6
3,4
Расположите свойства числовых характеристик случайных величин в следующем порядке: «математическое ожидание суммы двух случайных величин, математическое ожидание отклонения случайной величины от ее математического ожидания, дисперсия постоянной величины»:
1 M(x + y) = M(x) + M(y)
2 M(x – M(x)) = 0
3 σ² (c) = 0
Случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности, называется … случайной величиной
Установите соответствие между числовой характеристикой случайной величины и ее определением:
Математическое ожидание
Дисперсия
Среднеквадратическое отклонение
M(X) = x₁p₁ + x₂p₂ + ··· + xnpn = Σ
σ² = Σ (xi – M(x))² · pi
σ(X) = √σ²
В числе 0,0529 первой (левой) значащей цифрой является …
В числе 456,012 укажите цифру в разряде единиц …
Дробь 2/7 выразили десятичной дробью 0,29, тогда относительная погрешность такого приближения, выраженная в процентах равна …
2,7%
29%
0,43%
Количество значимых цифр в числе 5,094 равно …
4
3
5
Модуль разности точного и приближенного значений – это …
граница абсолютной погрешности измерения
относительная погрешность приближенного значения
абсолютная погрешность приближенного значения
Расположите числа в порядке возрастания количества значащих цифр:
1 0,0046
2 0,004600
3 1,23456
Сопоставьте характеристику точности приближенной величины и ее обозначение:
Абсолютная погрешность
Погрешность
Предельная абсолютная погрешность
Δ
Δa
Δa
Студенту необходимо округлить и определить абсолютную погрешность при округлении числа e с точностью до 0,01.
Укажите верное решение.
Нужно округлить число e до второго знака после запятой (т.е. иметь две верные цифры после запятой). Запишем число с достаточно большим количеством значащих цифр е=2,7182818284590. Так как справа от 1 стоит число 8, то получим е=2,72. Абсолютная погрешность (с точностью до 5-го знака после запятой) составит: Δa = 2,72 – 2,71828 = 0,00172, а так как 0,00172<0,005, можно утверждать, что стоящая во втором отрицательном разряде цифра 2 является верной.
Нужно округлить число е до третьего знака после запятой (т.е. иметь три верные цифры после запятой). Запишем число с достаточно большим количеством значащих цифр е=2,7182818284590. Так как справа от 8 стоит число 2, то получим е=2,718. Абсолютная погрешность (с точностью до 5- го знака после запятой) составит: Δa = 2,718 – 2,71828 = 0,00028, а так как 0,00028<0,005, можно утверждать, что стоящая во втором отрицательном разряде цифра 8 является верной.
Нужно округлить число е до второго знака после запятой (т.е. иметь две верные цифры после запятой). Запишем число с достаточно большим количеством значащих цифр е=2,7182818284590. Так как справа от 1 стоит число 8, то получим е=2,72. Абсолютная погрешность (с точностью до 5-го знака после запятой) составит: Δa = 2,72 – 2,71828 = 0,00672, а так как 0,00672>0,005, можно утверждать, что стоящая во втором отрицательном разряде цифра 2 является сомнительной.
Цифра числа называется … , если ее абсолютная погрешность не превосходит единицы разряда, в котором стоит эта цифра
Число 0,0172 имеет запись в нормальной форме …
1,72·10⁻³
1,72·10⁻¹
1,72·10⁻²
Число 1,544 округлили до 0,01, тогда относительная погрешность такого приближения в процентах равна …
0,26
0,65
0,11
… множества A называется множество всех элементов, не принадлежащих A (A = U\A)
Q – это множество … чисел
В числе 0,0172 первой (левой) значащей цифрой является …
Вероятность наступления некоторого события не может быть равна …
0
1
2
Вставьте выражения в логическом порядке для определения предела функции в точке: « … что из условия следует …»:
1 Ɐ ε > 0 ∃ δ > 0
2 |x – a| < δ
3 |f(x) – b| < ε
Две матрицы А и В называются … матрицами, если их размеры совпадают и их соответствующие элементы равны
Две прямые y₁ = 7x + 5 и y₂ = 7x – 5 на плоскости …
совпадают
перпендикулярны
параллельны
Действительная часть (ReZ) комплексного числа z = 3 + 5і равна …
Дискретная случайная величина Х имеет … закон распределения с параметрами n и p, если она принимает значения 0, 1, 2, …, m, …, n с вероятностями P(X=m)=Cnmpmqn-m, где 0 < p < 1, q = 1 – p
Для комплексных чисел 3 + 2i и 7 – 3і расположите результаты арифметических действий в следующем порядке: сумма, разность, произведение:
1 10 – i
2 –4 + 5i
3 27 + 5i
Дробь 1/6 выразили десятичной дробью 0,17, тогда относительная погрешность такого приближения, выраженная в процентах равна …
0,17%
40%
0,33%
Если y = f(x) – … функция на отрезке [a; b], то определенный интеграл ∫ f(x)dx существует
Если элементы двух строк (столбцов) матрицы … , то определитель равен нулю
Заданы множества А = (b, а), В = (a, 1, с), тогда декартовым произведением этих множеств А и В является множество …
{(b, а), (b, 1), (b, с), (a, а), (a, 1), (a, c)}
пустое множество
{(a, b), (c, a), (1, b), (1, a), (c, b), (c, 1)}
Задачей … называется задача нахождения такого решения уравнения, которое при x = x₀ принимает значение y = y₀
Закон распределения дискретной случайной величины задан следующей таблицей (см. ниже). Математическое ожидание равно …
-0,1
0,5
0
Закон распределения дискретной случайной величины задан таблицей (см. ниже). Значение функции распределения этой случайной величины на интервале 2 < x равно …
Значение выражения (4 – 3i) + (8 + 5i) равно …
2 + 12i
12 + 2i
–2 – 8i
Значение выражения i^10 равно …
Значение предела lim (5x³+x²+1) / (2x⁴−3x²+5x+2), x⟶∞ равно …
Значение производной функции y = ln(1 + 5x) в точке x₀ = 0 равно …
Игральный кубик бросают 4 раза. Случайная величина х — число выпадений 5 очков.
Возможные значения данной случайной величины – это …
4
1; 2; 3; 4; 5
0; 1; 2; 3; 4
Интеграл от алгебраической суммы функций, равен алгебраической … интегралов от этих функций
Каноническое уравнение прямой, проходящей через точки А(2,3) и В(7,5), имеет вид …
(x–2)/5 = (y–3)/2
(x–2)/6 = (y–3)/7
(x–1)/5 = (y+2)/2
Квадрат модуля комплексного числа 7 – 4і равен …
Комплексно-сопряженным для числа 7 – 2і является …
7 + 2i
–7 + 2i
–2 + 7i
Косинус угла между прямыми y₁ = 2x + 1 и y₂ = –x + 2 равен …
√10/10
√10/15
–√10/14
Кривая, состоящая из всех точек плоскости, разность расстояний от которых до двух данных точек (фокусов), взятая по абсолютной величине, есть величина постоянная, называется …
Кривая второго порядка, имеющая директрису – это …
Матрица А называется … , если ее определитель отличен от нуля
вырожденной
обратной
невырожденной
Матрица А называется … с матрицей В, если число столбцов матрицы А равно числу строк матрицы В
Мгновенная скорость материальной точки, движущейся прямолинейно по закону s = 2sin(4t – 4) в момент t=1 равна …
Неопределенный интеграл ∫(4x^9 – 2/x + 7sinx)dx равен …
4x^10 – lnx – cosxdx + C
2/5 x^10 – 2lnx – 7cosx + C
x^10 – 2lnx + 7cosx + C
Неопределенный интеграл ∫ dx / (x²+4x+5) равен …
arcsin(x + 2) + C
arctg(x + 2) + C
sin(x + 2) + C
Несколько событий называются … , если возможно появление нескольких событий одновременно
Общее решение дифференциального уравнения y’ + y = 0 имеет вид …
y = e⁻²ˣ + C
y = Ce⁻ˣ
y = eˣ
Общее решение дифференциального уравнения y” – 6y’ + 9y = 0 имеет вид …
y = e⁻³ˣ (C₁ + C₂x)
y = C₁e⁻³ˣ + C₂x
y = C₁e⁻³ˣ
Определенный интеграл ∫ 1 / √(x + 1) dx, x=0..1 равен …
2√2
2√2 – 2
–2√2
Определенный интеграл ∫ f(x)dx, x=2..2 равен …
Отношение абсолютной погрешности к модулю приближенного значения — это …
относительная погрешность приближенного значения
граница абсолютной погрешности измерения
относительная погрешность точного значения
Переменная величина, которая принимает значения, зависящие от исходов испытания (то есть в зависимости от случая) – это … величина
Предел lim (x²−2x) / (x²−4), x⟶2 равен …
0,5
0,7
0
Предел функции lim (2 + 3x + 4x²) / (x + 2x² + 1), x⟶∞ равен …
Предел функции lim (25 – x²) / (x² – 5x), x⟶5 равен …
2
0
-2
Предел функции lim x / (√(x + 4) – 2), x⟶0 равен …
При пересечении двух множеств получаем третье множество, которое …
всегда состоит из одного элемента
может состоять из одного элемента
всегда не содержит элементов
Произведение комплексных чисел (3 – 2i)(2 + 5i) равно …
11 – 16i
6 – 10i
16 + 11i
Производная функции 2x⁴ − tgx в точке x=0 равна …
1
0
-1
Производной функции f ‘(x) называется …
Δf(x)
Δf(x) / Δx
lim Δf(x) / Δx, Δx⟶0
Процесс нахождения первообразной для данной функции называют …
Пусть дана система уравнений A = {2x₁ + x₂ − 2x₃ = 9, 3x₁ − 2x₂ + x₃ = 2, x₁ + x₂ − 4x₃ = 11, тогда определитель |A| этой системы равен …
Пусть дана система уравнений A = {2x₁ + x₂ − 2x₃ = 9, 3x₁ − 2x₂ + x₃ = 2, x₁ + x₂ − 4x₃ = 11, тогда определитель |A₁| этой системы равен …
33
34
35
Пусть дана система уравнений A = {2x₁ + x₂ − 2x₃ = 9, 3x₁ − 2x₂ + x₃ = 2, x₁ + x₂ − 4x₃ = 11, тогда определитель |A₂| этой системы равен …
Пусть дана система уравнений A = {2x₁ + x₂ − 2x₃ = 9, 3x₁ − 2x₂ + x₃ = 2, x₁ + x₂ − 4x₃ = 11, тогда определитель |A₃| этой системы равен …
-33
-34
-35
Пусть дана система уравнений A = {2x₁ + x₂ − 2x₃ = 9, 3x₁ − 2x₂ + x₃ = 2, x₁ + x₂ − 4x₃ = 11, тогда решение (x₁, x₂, x₃) этой системы равно …
(2,1,2)
(-2,-1,-2)
(2,1,-2)
Расположите в порядке возрастания вероятности следующих событий:
1 игральный кубик бросили один раз, какова вероятность выпадения цифры 3
2 игральный кубик бросили один раз, какова вероятность выпадения четной цифры
3 игральный кубик бросили один раз, какова вероятность выпадения цифры меньше 5
Расположите действия в логическом порядке для нахождения промежутков возрастания или убывания функции у = f(х):
1 найти область определения D(f) функции у = f(x)
2 найти производную функции f ‘(x)
3 найти критические точки, где f ‘(x) = 0 или f ‘(x) не существует
Расположите действия при решении системы уравнений методом Гаусса в логическом порядке (первое действие, второе действие и т.д.):
1 составить расширенную матрицу системы
2 с помощью элементарных преобразований привести расширенную матрицу системы к ступенчатому виду
3 на основе полученной ступенчатой матрицы составить и решить систему линейных уравнений
Расположите дифференциальные уравнения в следующем порядке: «дифференциальное уравнение 1-го порядка, линейное однородное дифференциальное уравнение 2-го порядка, линейное неоднородное дифференциальное уравнение 2-го порядка»:
1 −12x + y’ + 6y = 0
2 -3 y” + 2y’ + 3y = 0
3 2y” – y’ + 5y = x²
Расположите значения интегралов в порядке возрастания:
1 ∫ x³dx, x=0..1
2 ∫ 3x²dx, x=0..1
3 ∫ 4xdx, x=0..2
Расположите значения миноров M₁₁, M₁₃, M₂₁, M₃₂ матрицы A = ((2, −7, 3), (4, 5, −2), (−8, 1, −3)) в порядке убывания:
1 M₁₃
2 M₂₁
3 M₁₁
4 M₃₂
Расположите значения производных для функций в следующем порядке: «y = sinx, y = cosx, y = lnx»:
1 y’ = cosx
2 y’ = −sinx
3 y’ = 1/x
Расположите множества в порядке убывания количества их элементов:
1 множество действительных чисел
2 множество рациональных чисел
3 множество натуральных чисел
Расположите первообразные для данных функций в следующем порядке: «5x⁴, 6x⁵, 7x⁶»:
1 x⁵ + C
2 x⁶ + C
3 x7 +C
Расположите результаты умножения матрицы A = ((3, 4), (0, −7), (−2, 5)) на число α в порядке α = 2, α = −3, α = 5, α = −5:
1 ((6, 8), (0, −14), (−4, 10))
2 ((−9, 12), (0, 21), (6, −15))
3 ((15, 20), (0, −35), (−10, 25))
4 ((−15, −20), (0, 35), (10, −25))
Расположите уравнения кривых второго порядка в следующем порядке: «эллипс, окружность, гипербола»:
1 x²/9 + y²/5 = 1
2 (x + 2)² + (y – 1)² = 1²
3 x²/9 – y²/1 = 1
Расположите формулы, выражающие свойства дисперсии в следующем порядке: «дисперсия от константы, дисперсия разности двух независимых случайных величин, дисперсия произведения двух независимых случайных величин»:
1 σ²(c) = 0
2 σ²[X – Y] = σx² + σy²
3 σ²[XY] = σx²σy² + (M(x))²σy² + (M(y))²σx²
Расположите формулы в следующем порядке: «первый замечательный предел, второй замечательный предел, предел отношения двух функций»:
1 lim sinx/x, x⟶0 = 1
2 lim (1 + 1/x)ˣ, x⟶∞ = lim (1 + x)^(1/x), x⟶0 = e
3 lim f(x)/g(x) = lim f(x) / lim g(x)
Расположите формулы в следующем порядке: «формула сложения вероятностей для совместных событий, формула умножения вероятностей, формула классической вероятности»:
1 P(A + B) = P(A) + P(B) – P(AB)
2 p(A₁A₂ … An) = p(A₁) · p(A₂) · … · p(An)
3 P(A) = m/n
Расположите числа в порядке возрастания количества значащих цифр:
1 0,0016
2 0,712
3 45,03
Результат вычисления интеграла ∫ x⁴dx, x=1..3 равен …
1/5
243
242/5
Соотнесите арифметические действия с их результатами:
2i * (5 + 3i)
(5 + 3i)²
(5 + 3i) * (–6 + 4i)
–6 + 10i
16 + 30i
–42 + 2i
Сопоставьте арифметическое действие и его результат:
(–3 – 2i) + (5 + 3i)
(–3 – 2i) – (5 + 3i)
(–3 – 2i) * (5 + 3i)
2 + i
–8 – 5i
–9 – 19i
Сопоставьте взаимное расположением прямых y₁ = k₁x + b₁ и y₂ = k₂x + b₂ на плоскости и их условие:
Прямые параллельны
Прямые перпендикулярны
Прямые совпадают
k₁ = k₂, b₁ ≠ b₂
k₁ ∙ k₂ = –1
k₁ = k₂, b₁ = b₂
Сопоставьте законы над множествами и их описание:
A ∪ B = A ∩ B; A ∩ B = A ∪ B}
A ∪ (A ∩ B) = A; A ∩ (A ∪ B) = A}
(A ∩ B) ∪ (A ∩ B) = A; (A ∪ B) ∩ (A ∪ B) = A}
законы де Моргана
законы поглощения
законы склеивания
Сопоставьте интеграл от элементарной функции и его значение:
∫ eˣ dx
∫ cosx dx
∫ dx / sin²x
eˣ + C
sinx + C
-ctgx + C
Сопоставьте математическое высказывание и его обозначение:
Элемент принадлежит множеству
Множество включено в другое множество
Элемент не принадлежит множеству
a ∈ A
A ⊂ B
a ∉ A
Сопоставьте матрицу и ее вид:
((1, 2, 3), (2, 1, 3), (3, 1, 2))
((0, 0, 0), (0, 0, 0), (0, 0, 0))
((1, 0, 0), (0, 1, 0), (0, 0, 1))
((3, 0, 0), (2, 4, 0), (5, 1, 5))
квадратная матрица
нулевая матрица
единичная матрица
нижняя треугольная матрица
Сопоставьте понятие в определении неопределенного интеграла (∫ f(x)dx = F(x) + C) и его обозначение:
Переменная интегрирования
Подынтегральная функция
Первообразная
x
f(x)
F(x)
Сопоставьте правую часть нелинейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами и его частное решение:
f(x) = aemx, m ≠ k₁ ≠ k₂
f(x) = aemx, m = k₁
f(x) = ax² + bx + c
ỹ = Aemx
ỹ = Axemx
ỹ = Ax² + Bx + C
Сопоставьте свойства пределов и их значения:
lim c, x⟶x₀
lim (f(x) ⋅ g(x)), x⟶x₀
lim (f(x) − g(x)), x⟶x₀
0
lim f(x), x⟶x₀ ⋅ lim g(x), x⟶x₀
lim f(x), x⟶x₀ − lim g(x), x⟶x₀
Сопоставьте свойство определенного интеграла и его запись:
Постоянный множитель можно выносить за знак интеграла
Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций
Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей
∫af(x)dx = a∫f(x)dx
∫(f(x) ± g(x)) = ∫f(x)dx ± ∫g(x)dx
∫f(x)dx = ∫f(x)dx + ∫f(x)dx
Сопоставьте событие и его вероятность:
Событие A – случайное
Событие A – достоверное
Событие A – невозможное
0 ≤ p(A) ≤ 1
p(A) = 1
p(A) = 0
Сопоставьте событие и его характеристику:
При бросании игрального кубика выпадет меньше 7 очков
При бросании игрального кубика выпадет больше 7 очков
При бросании игрального кубика выпадет меньше 5 очков
достоверное событие
невозможное событие
случайное событие
Сопоставьте способ задания прямой на плоскости и ее уравнение:
Известны точка M(x₀, y₀) и угловой коэффициент k
Известны точки A(x₁, y₁) и B(x₂, y₂)
Известны отрезки a и b
y = y₀ + k(x − x₀)
(x − x₁)/(x₂ − x₁) = (y − y₁)/(y₂ − y₁)
x/a + y/b = 1
Сопоставьте характеристику точности приближенной величины и ее формулу:
Абсолютная погрешность
Относительная погрешность
Предельная относительная погрешность
Δ = |A – a|
δ = Δ / |a|, a ≠ 0.
δa = Δa / |a|, a ≠ 0.
Сопоставьте числовую характеристику случайной величины и ее определение:
Математическое ожидание
Дисперсия
Среднеквадратическое отклонение
среднее значение случайной величины
мера разброса значений случайной величины относительно его математического ожидания
квадратный корень из дисперсии
Сумма координат точки пересечения прямых y₁ = 3x + 2 и y₂ = –2x + 3 равна …
Угол наклона к оси абсцисс касательной к графику функции y = 2x⁴ в точке с абсциссой x₀ = 0,5 равен …
45°
90°
30°
Уравнение ((x+1)²/16) – ((y+2)²/25) = 1 задает …
гиперболу с центром в точке O (-1; -2)
параболу с центром в точке O (1; 2)
эллипс с центром в точке O (1; 2)
Уравнение прямой с угловым коэффициентом, проходящей через точки А(2,3) и В(7,5), имеет вид …
y = 0,4x – 3,2
y = 0,4x – 2,2
y = 0,4x + 2,2
Уравнение эллипса, полуоси которого равны a = 3, b = 2, имеет вид …
x²/9 + y²/4 = 1
x²/3 + y²/2 = 1
x²/2 + y²/3 = 1
Фокусы гиперболы находятся на …
действительной оси внутри гиперболы
мнимой оси
действительной оси снаружи гиперболы
Функция f(x) имеет устранимый разрыв в точке x = 3 и lim f(x) = 2, x⟶3−0, тогда lim f(x), x⟶3+0 равен …
0
-2
2
Функция у = f(x) называется … функцией на множестве D, если для любых x₁, x₂ ϵ D из неравенства x₁ < x₂ следует неравенство f(x₁) > f(x₂)
Центр эллипса (x–3)²/10 + (y+1)²/5 = 1 находится в точке …
(3; 1)
(3; –1)
(10; 5)
Число, равное наивысшему порядку минора матрицы, называется …
ранг матрицы
определитель матрицы
базис матрицы
Число 1,97 округлили до единиц, тогда относительная погрешность такого приближения в процентах равна …
15%
1,5%
0,1%
Число 3,12 округлили до единиц, тогда относительная погрешность такого приближения в процентах равна …
3,12%
30%
3,85%
Число k в интеграле ∫7e²ˣdx = ke²ˣ + C равно …
2/3
7/3
7/2
Выберите верное доказательство того, что функция f(x) = x² – 1 непрерывна в точке x = 4.
Найдем значение функции в точке x = 4, f(4) = 15.
Вычислим предел: lim (x² – 1) = lim x² – lim 1 = 16 – 1 = 15.
Получили, что предел функции в точке x = 4 равен значению функции в этой точке. Это означает, что условие непрерывности функции в точке выполнено, следовательно, данная функция непрерывна в точке x = 4.
Найдем значение функции в точке x = 0, f(0) = 0.
Вычислим предел: lim (x² – 1) = lim x² – lim 1 = 16 – 1 = 15.
Получили, что предел функции в точке x = 0 не равен значению функции в этой точке. Это означает, что условие непрерывности функции в точке выполнено, следовательно, данная функция непрерывна в точке x = 4.
Найдем значение функции в точке x = 4, f(4) = 15.
Вычислим предел: lim (x² – 1) = lim x² – lim 1 = 1 – 1 = 0.
Получили, что предел функции в точке x = 4 равен 0, а значение функции в этой точке равно 15. Это означает, что условие непрерывности функции в точке выполнено, следовательно, данная функция непрерывна в точке x = 4.
Дан неопределенный интеграл ∫sin(5x + 4)dx.
Укажите верное рассуждение для его решения.
Введем новую подстановку, положив u = 5x + 4, du = (5x + 4)’dx = 5dx, dx = 1/5 du.
Введем новую подстановку, положив u = sinx, du = (sinx)’dx = cosxdx, dx = (5x + 4)du.
Подстановку вводить не нужно, это табличный интеграл.
Дан неопределенный интеграл ∫x³lnxdx.
Решите его методом по частям и укажите верный ответ.
(lnx) x/4 – 1/16 x + C.
x⁴/4 – 1/16 x⁴ + C.
(lnx) x⁴/4 – 1/16 x⁴ + C.
Дан определенный интеграл ∫x²dx, x=1..2.
Укажите верное решение.
∫x²dx = x³/6 |₁² = 8/6 – 1/6 = 7/6.
∫x²dx = x³/3 |₁² = 8/3 – 1/3 = 7/3.
∫x²dx = x³/3 |₁² = 6/3 – 3 = –1.
Дан предел lim ˣ√(1 + 5x), x→0.
Выберите верное рассуждение для решения данного предела.
lim ˣ√(1 + 5x) = lim (1 + 5x)ˣ = [1ˣ] = lim (1 + 5x) = e0 =1.
lim ˣ√(1 + 5x) = lim (1 + 5x)1/ˣ = [1∞] = lim (1 + 5x)^(1/5x)⁵ = e⁵.
lim ˣ√(1 + 5x) = lim (1 + 5x)1/ˣ = [1∞] = lim (1 + 5x)0 = 0.
Дан чертеж (см. ниже).
По данному чертежу вычислите площадь плоской фигуры, используя формулу S = ∫(f₂(x) – f₁(x))dx, x=a..b.
9/2.
7/2.
11/2.
Дана гипербола x²/25 – y²/64 = 1.
Запишите уравнение ее директрис и асимптот.
Уравнение директрис x = ±16/√41; уравнение асимптот y = ±5/4 x.
Уравнение директрис x = ±25/√41; уравнение асимптот y = ±5/4 x.
Уравнение директрис x = ±41/√16; уравнение асимптот y = ±5/4 x.
Дана система уравнений {5x₁ − 2x₂ + 4x₃ = 5, 2x₁ + 3x₂ − x₃ = 7, 3x₁ − x₂ + 2x₃ = 3.
Решите систему уравнений методом Крамера.
x₁ = −1, x₂ = 2, x₃ = −1.
x₁ = −1, x₂ = −2, x₃ = −1.
x₁ = 1, x₂ = 2, x₃ = 1.
Дана система уравнений {x₁ + 2x₂ + 3x₃ = 1, 2x₁ − 1x₂ + 2x₃ = 6, x₁ + x₂ + 5x₃ = −1.
Укажите ступенчатую матрицу, полученную при решении данной системы методом Гаусса.
((1, 0, 0, 4), (0, 1, 0, 0), (0, 0, 1, –1)).
((1, 0, 0, –4), (0, 1, 1, 0), (0, 0, 1, –1)).
((1, 2, 3, 4), (0, 1, 0, 0), (0, 0, 1, 1)).
Дана функция у = eˣ / sinx.
Найдите производную функции, используя правило дифференцирования отношения двух функций.
eˣ (sinx + cosx) / sin²x.
eˣ (sinx – cosx) / sin²x.
eˣ (sinx – cosx) / sinx.
Дана функция y = lgx – 8tgx.
Найти производную функции.
1/xln10 – 8/cos²x.
1/xln10 + 8/cos²x.
1/xln10 – 8/cosx.
Дано дифференциальное уравнение 2уу’ = 1 – 3х².
Решите его и укажите верный вид общего решения.
y² = Cxe⁻ˣ.
y² = x – x³ + C.
y = x – x³.
Дано дифференциальное уравнение y” + 6y’ + 8y = 0.
Решите его и укажите верный вид общего решения.
y = (C₁e⁻²ˣ + C₂e⁻⁴ˣ).
y = C₁e⁻³ˣ + C₂e⁻⁴ˣ.
y = (C₁eˣ + C₂e⁻⁴ˣ).
Даны две прямые на плоскости x – 3y + 5 = 0 и 2x + 4y – 7 = 0.
Найдите угол между этими прямыми.
90°.
45°.
120°.
Даны множества А={11;12;43;54;7}, В={7;12}.
Найдите дополнение к множеству В до множества А.
A \ B = (11;43;54}.
A \ B = {7;12}.
A \ B = {11;43;54;7;12}.
Длина детали представляет собой нормально распределенную случайную величину с математическим ожиданием 40 мм и средним квадратическим отклонением 3 мм.
Найдите вероятность того, что длина произвольно взятой детали будет больше 34 мм и меньше 43 мм.
P(α ≤ X ≤ β) = ∫f(x)dx; P(α ≤ X ≤ β) = Ф((β – a)/σ) – Ф((α – a)/σ)
P(34 ≤ X ≤ 43) = Ф((43 – 40)/3) – Ф((34 – 40)/3) = Ф(2) – Ф(–2) =
= Ф(1) + Ф(2) = 0,4772 + 0,4772 = 0.
P(α ≤ X ≤ β) = ∫f(x)dx; P(α ≤ X ≤ β) = Ф((β – a)/σ) – Ф((α – a)/σ)
P(34 ≤ X ≤ 43) = Ф((43 – 40)/3) – Ф((34 – 40)/3) = Ф(1) – Ф(–2) =
= Ф(1) + Ф(2) = 0,3413 + 0,4772 = 0,8185.
P(α ≤ X ≤ β) = ∫f(x)dx; P(α ≤ X ≤ β) = Ф((β – a)/σ) – Ф((α – a)/σ)
P(34 ≤ X ≤ 43) = Ф((43 – 40)/3) – Ф(0) = Ф(1) – Ф(0) =
= Ф(1) + Ф(2) = 0,3413 + 0 = 0,3413.
Для приближенного числа х=72,356 известна абсолютная погрешность Δа = 0,04.
Определите его верные значащие цифры.
Верными являются цифры 7; 2; 3; 5.
Верными являются цифры 7; 2; 3.
Верными являются цифры 7; 2; 3; 5; 6.
Из n аккумуляторов за год хранения k выходит из строя. Наудачу выбирают аккумуляторов. Дано: n = 100, k = 7, m = 5, l = 3.
Определите вероятность того, что среди аккумуляторов m-l исправных, используя формулу Бернулли.
0,0847.
0,0564.
0,0394.
На каждой из пяти одинаковых карточек напечатана одна из следующих букв: «а», «м», «р», «т», «ю». Карточки тщательно перемешаны.
Найдите вероятность того, что на четырех вынутых по одной карточке можно прочесть слово «юрта».
1/120.
1/12.
1/6.
На плоскости даны прямая y = 4/3x – 4 и точка A(1, –4).
Найдите расстояние от прямой до точки.
0,8.
0,6.
0,4.
Преподаватель на экзамене попросил студента найти определитель транспонированной матрицы к матрице A = ((1, –1, 2), (3, 4, –5), (7, –9, –8)).
Что должен ответить студент?
-167
-176
-177
Преподаватель на экзамене попросил студента представить комплексное число z = (5+i) / ((1+i)(2–3i)) в виде a + bi.
Что должен ответить студент?
12/13 + 5/13i.
11/13 + 15/13i.
12/18 + 5/18i.
Пусть дана матрица A = ((1, 2, 3), (2, 1, 3), (3, 2, 1)).
Чему будет равна сумма миноров M₂₂ + M₃₃ ?
-11
-12
-13
Студенту на экзамене попался вопрос: «Число z⁻1, обратное числу z = 3 – i – это …».
Что должен ответить студент?
–0,3 + 0,1i.
0,3 – 0,1i.
0,3 + 0,1i.