Численные методы тест Синергия/МОИ/ МТИ ответы на все 50 вопросов из теста по данной дисциплине. Результат 93 балла из 100 баллов Отлично.
купить ответы по ссылке: ССЫЛКА НА ОТВЕТЫ
Заказать сдачу тестов – консультация бесплатно: sinerqy@yandex.ru
Тема 2. Решение алгебраических и трансцендентных уравнений
Тема 3. Решение систем линейных алгебраических уравнений. Решение систем нелинейных уравнений
Тема 4. Аппроксимация функций
Тема 5. Интерполяция
Тема 6. Численное интегрирование
Тема 7. Численное решение обыкновенных дифференциальных уравнений
… метод применяется, если для получения результата требуется довольно ограниченное количество вычислений и если известен диапазон, в котором справедливо решение
Графический
Аналитический
Численный
…dx – это отношение абсолютной погрешности Dx к модулю приближенного значения x¢
Тип ответа: Текcтовый ответ
В методе Гаусса приведение системы линейных уравнений к треугольному виду это …
обратный ход
прямой ход
простая итерация
двойной пересчет
В основе метода … лежит использование разложения функций в ряд Тейлора, причем члены, содержащие вторые и более высоких порядков производные, отбрасываются
Ньютона–Рафсона
Рунге–Кутта
Лагранжа
Ньютона–Лейбница
Во многих случаях, когда функция задана аналитически, определенный интервал вычисляется по формуле …
Крамера
Ньютона–Лейбница
Лагранжа
Рунге–Кутта
Остроградского–Гаусса
Вычислительные методы делятся на прямые и …
Тип ответа: Текcтовый ответ
Для приведенной ниже системы линейных алгебраических уравнений (СЛАУ) свободные члены системы – это …
x1, x2 … xn
b1, b2 … bn
Для приведенной ниже системы линейных алгебраических уравнений (СЛАУ) a₁₁a₁₂ … aₙₙ – это …
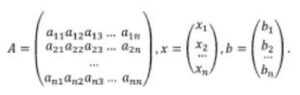
постоянные коэффициенты
неизвестные
свободные члены системы
Для решения систем линейных уравнений с трехдиагональной матрицей используется метод …
итераций
коллокации
прогонки
квадратных корней
Гаусса
Если выразить относительную погрешность (x) через абсолютную погрешность x и модуль приближенного значения x, получим: …
dx = Dx |x¢|
dx = Dx – |x¢|
δx = Δx / |x’|
Если коэффициенты ai функции j(x) определяются из условия равенства f(xi) = j(xi), т.е. функции совпадают в заданных известных точках, то такой способ аппроксимации называется …
Тип ответа: Текcтовый ответ
Если на всем интервале строится одна функция – это … интерполяция
кусочная
локальная
глобальная
Задача … функции заключается в том, чтобы для данной функции построить другую, отличную от нее функцию, значения которой достаточно близки к значениям данной функции
Тип ответа: Текcтовый ответ
Используя графические методы решения задач в математике, …
можно найти решение задачи с помощью формулы или ряда формул
в ряде случаев можно оценить порядок искомой величины, например, найти с определенной точностью корни алгебраического уравнения
можно свести решение задачи к выполнению конечного количества арифметических действий над числами, при этом результаты получаются в виде числовых значений
Итерационным численным методом приближенного нахождения корня уравнения является метод …
половинного деления
простых итераций
касательных
хорд
К группе прямых методов относят …
Тип ответа: Множественный выбор
метод простых итераций
метод Гаусса
метод хорд
метод Крамера
Метод … это способ решения систем линейных алгебраических уравнений с числом уравнений, равным количеству неизвестных с ненулевым главным определителем матрицы коэффициентов системы
Крамера
Гаусса
простых итераций
Метод … также известен как метод касательных
Ньютона
Эйлера
Лагранжа
Симпсона
Метод … является наиболее простым численным методом решения порядок точности (систем) обыкновенных дифференциальных уравнений и имеет первый порядок точности
Эйлера
Рунге–Кутта
Симпсона
Метод бисекции – это другое название метода …
половинного деления
прогонки
Гаусса
касательных
Метод Гаусса и метод Крамера для систем линейных алгебраических уравнений относятся к … методам решения задач в математике
графическим
аналитическим
численным
Метод прогонки состоит из … этапов
двух
трех
четырех
Метод простых итераций является …
самым простым и надежным способом решения нелинейного уравнения
популярным способом численного решения математических задач
итерационным численным методом приближенного нахождения корня уравнения
Метод решения задачи называется итерационным, если …
он позволяет получить решение после выполнения конечного числа элементарных операций
его смысл заключается в построении последовательных приближений к решению задачи
он позволяет получить решение после выполнения не более 10 элементарных операций
Метод решения задачи называется простым, если …
он позволяет получить решение после выполнения конечного числа элементарных операций
его смысл заключается в построении последовательных приближений к решению задачи
он позволяет получить решение после выполнения не более 3 элементарных операций
Метод трапеций, метод прямоугольников и метод простых итераций относятся к … методам решения задач
графическим
аналитическим
численным
Метод хорд является … численным методом приближенного нахождения корня уравнения
Тип ответа: Текcтовый ответ
Многочисленные приближенные методы решения систем линейных алгебраических уравнений делятся на две большие группы – … методы и методы итераций
Тип ответа: Текcтовый ответ
На данный момент … решения систем нелинейных уравнений в общем виде
существует два прямых метода
существует три прямых метода
существует четыре прямых метода
не существует прямых методов
Наиболее эффективным методом решения нелинейных уравнений является метод …
простых итераций
касательных
хорд
Найти с определенной точностью корни алгебраического уравнения можно с помощью … методов
графических
аналитических
численных
Неверно, что к итерационным методам относится метод …
простой итерации
Зейделя
последовательной релаксации
половинного деления
Неверно, что к методам решения нелинейного уравнения относится метод …
половинного деления
простых итераций
Ньютона
Крамера
хорд
Неверно, что к методам численного интегрирования относят метод …
прямоугольников (левых, правых, средних)
трапеций
парабол
простой итерации
Неверно, что к прямым методам решения систем линейных алгебраических уравнений относят такие методы, как …
Тип ответа: Множественный выбор
метод половинного деления
метод Гаусса
метод Крамера
метод простых итераций
Необходимым и достаточным условием существования единственного решения системы линейных уравнений является неравенство нулю определителя матрицы коэффициентов, а в случае если определитель матрицы равен нулю, …
матрица называется треугольной
матрица называется вырожденной
система называется плохо обусловленной
Одним из основных численных методов является метод …, на принципах которого основаны остальные методы
половинного деления
итераций
касательных
хорд
Определение аппроксимирующей функции представляет собой задание вида функций и нахождение …
ее коэффициентов
значения собственных чисел
ее значения
При аппроксимации многочленами предварительно задаются степенью многочлена и находят его коэффициенты, при этом отклонение (x) от f(x) …
должно быть наименьшим
может быть любым
должно быть наибольшим
При сложении или вычитании складываются … погрешности
абсолютные
относительные
как относительные, так и абсолютные
Приближение функции также называют … функции
Тип ответа: Текcтовый ответ
Приведенная ниже формула показывает, как получается полином любого порядка при интерполировании функций с помощью метода …
Эйлера
Симпсона
метода Рунге–Кутта
Лагранжа
Процесс итераций сходится при условии …
|j¢(c)| > 1
|j¢(c)| ³ 0
|j¢(c)| < 1
Решением дифференциального уравнения называется всякая функция y = (x), которая после ее подстановки в уравнение превращает его в …
Тип ответа: Текcтовый ответ
Согласно теореме …, если функция f(x) непрерывна на отрезке [a, b], то для любого e > 0 существует многочлен j(x) степени m = m(e), абсолютное отклонение которого от функции f(x) на отрезке [a, b] меньше e
Коши
Вейерштрасса
Гюа
Ролля
Содержать некоторую погрешность (ошибку) может решение, получаемое … методом решения задач
графическим или аналитическим
аналитическим
численным
Сущность методов конечных разностей состоит в том, что область непрерывного изменения аргумента и функции заменяется дискретным множеством точек, называемых …, которые составляют разностную сетку
Тип ответа: Текcтовый ответ
Условием существования корня непрерывной функции на интервале является …, что говорит о том, что на данном интервале функция изменяет знак, т.е. пересекает ось x
f(a) ∙ f(b) < 0
f(a) / f(b) = 0
f(a) + f(b) < 0
f(a) f(b) > 0
Уточнение корня – это вычисление приближенного значения корня с заданной точностью …
e > 0
e < 0
e = 0

